Dear Reader!

This is the third part in a series of articles about Variational Quantum Algorithms (VQAs). The first two parts were about specific algorithms – VQE and QAOA and in this part I’d like to explain the general structure as well as different components of such algorithms.

Before we begin, let’s just explain what a VQA is:

VQA is an algorithm which tries to find the minimum value of some function using:

• A parametrized quantum circuit as one of the steps for calculating a function’s value.
• Classical optimization to find the optimal parameters of the circuit.

If you want to read a more detailed definition I recommend Jhonathan Romero Fontalvo’s dissertation, section 1.2.

Also, two more things just to set the expectations right:

1. I’ve written this assuming running the programs on an actual QPU (Quantum Processing Unit), not a simulator. Accounting for both cases made some of the diagrams harder to read and it’s pretty straightforward to imagine what changes are needed if we run it on a simulator.
2. This is a popular article aimed at explaining the complexity of VQAs. It’s not a scientific paper and some of the choices I made might turn out to not be the most universal or 100% correct. In such cases please leave a comment, I’d love to discuss it.

With that being said, let’s get started with the

Basic setup

When I first started learning about Variational Quantum Algorithms (VQAs), I wasn’t able to appreciate how complex they are.

In my mind, a quantum algorithm looked like this:

Note: “backend” is a jargon term people in QC use for different hardware devices and their interfaces.

However, when I started learning and thinking more about running such algorithms on near-term quantum computers, I quickly realized this view is oversimplified; there are several crucial intermediate steps in a VQA that must be taken to make the best use of today’s devices.

One of the important questions one needs to ask is “How do I know what circuit I need to run?” The choice of the circuit is mainly motivated by the problem we want to solve and in the case of VQAs, we use so-called “Ansatz circuits” (see VQE article for more details). You can think about it as a circuit template – it has some parameters which correspond (directly or indirectly) to parameters of gates as well as some “hyperparameters” – e.g. the number of layers, the types of gates for a given layer, etc.

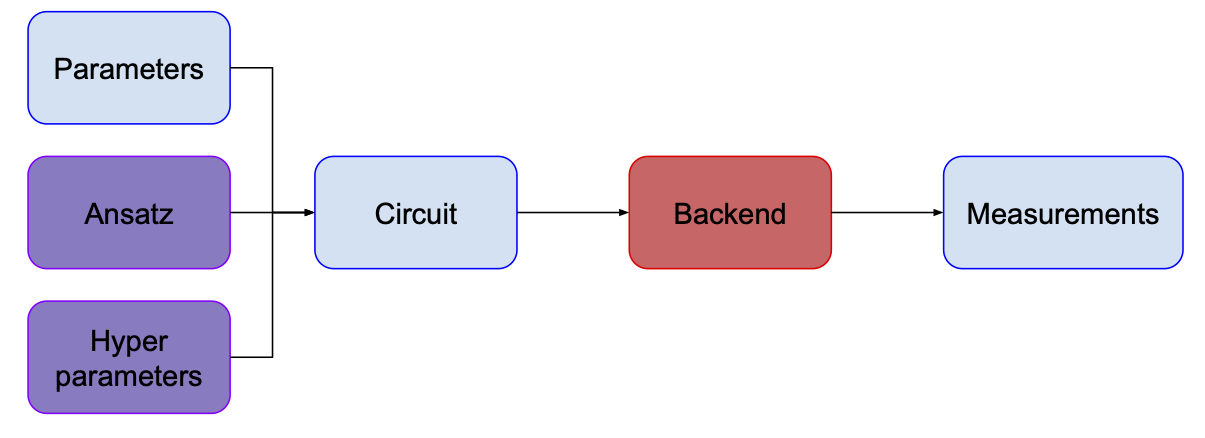
As you can see on the diagram, I’m using different colors for different blocks. Here’s what they mean:

1. Blue boxes are objects created/changed when we run the algorithm.
2. Purple boxes are objects which define the problem we’re solving and algorithm’s hyperparameters.
3. Green boxes are objects which can perform some actions. They change the content of the blue boxes and the way they do it is informed by the purple ones.
4. Backend is red, because it’s the actual quantum computer and I wanted it to stand out :)

In addition to the specific problem, the choice or design of the quantum circuit is determined by the backend/device. Devices we have available today cannot execute any quantum circuit we can imagine. The two main reasons for that are:

• Implemented (or “native”) gate sets – in the classical Boolean logic, people sometimes say that the NAND gate is a “universal” gate. This means that you can construct any circuit using only NAND gates. In quantum computing, it’s slightly more complicated. From what I’ve seen, usually a set of three gates is used to construct a universal set, but there are some schemes which involve 2 gates (or as it turns out even 1 gate!) (see wiki and here’s some more discussion on this topic). There are many different gate sets that you use for that purpose that are (at least on paper) equally good. But when you start implementing them on the real hardware, it turns out that some of these gates are easier to realize than others. So usually, when it comes to running a program on an actual quantum computer, you have only a handful of gate types available.
• Connectivity – in the ideal case, you assume that all the qubits are connected to each other. But in reality, this is often not the case – for example that would be infeasible for superconducting chips. Imagine having a chip where qubits are arranged in a line. Directly performing a CNOT gate on the first and last qubits is not possible, because these two qubits are not connected.

We can overcome these device-imposed restrictions by introducing an additional step that translates an “abstract circuit” into an “executable circuit”, which is called compilation. In the diagram below, I’ve hidden the connectivity and available gate set under “QPU specs” box (since it depends on the specific backend we’re using I added a dashed line to indicate causation).

I’ve also added a new box “Execution”, to make the diagram more consistent and clear.

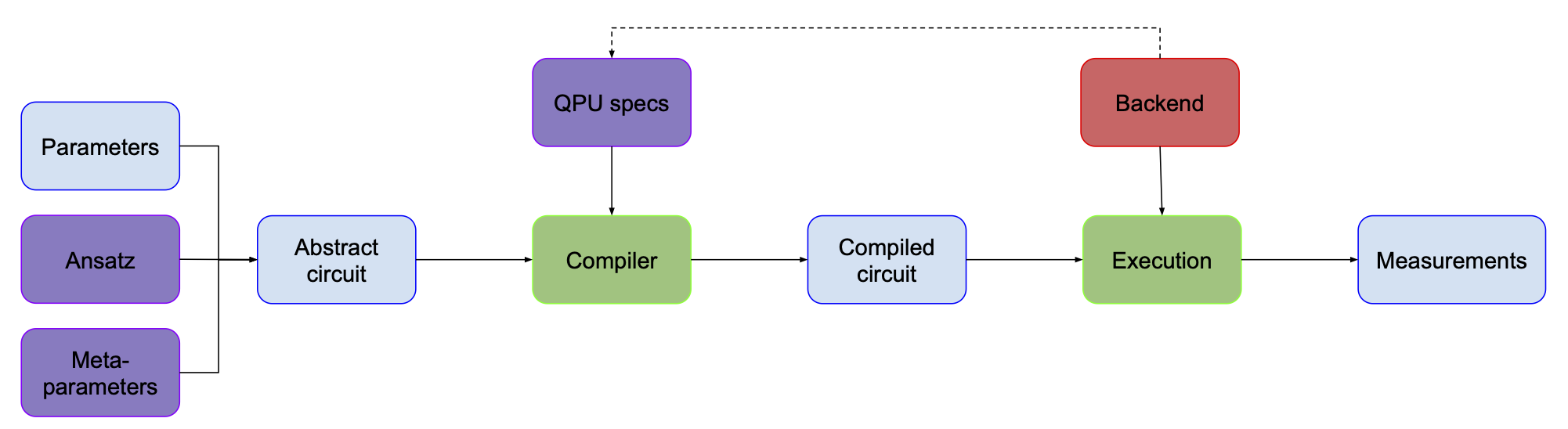
There’s one last step from the first picture that we haven’t talked about yet – getting measurements.

This one’s trivial, isn’t it? You just take a circuit, run it on your backend and measure the output, right?

Well, not necessarily. There are a couple of things to consider.

First, readout correction. As we mentioned before, quantum computers nowadays are imperfect machines. There’s no reason to think that these imperfections have spared the measurement process. When you measure your qubit, various errors can happen. Sometimes it’s impossible to say whether an error occurred, but sometimes we can detect its occurrence based on how the physical system has behaved. Then we can either discard such a sample or correct it. It is worth mentioning that measurement errors can be an order of magnitude higher compared with other types of errors (see this talk).

It is a good place to mention other types of error mitigation or error correction. In the most basic form it doesn’t need to be used for VQAs, as they are designed to be somewhat resistant to noise. While they can benefit from it (see e.g. here), I’m leaving it out from our discussion. Adding error correction is what I would consider an advanced modification of basic VQA, which is outside of the scope of this article. An additional complication is that depending on implementation it could live in different places in our diagram – e.g. ansatz or compilation.

Second, as you might remember from the VQE article, for a given Hamiltonian we need to measure each Pauli term separately, i.e. we need to run a separate circuit. However, this is the most naïve approach – in reality, there are certain grouping strategies that make it possible to measure multiple terms simultaneously. This also means that choosing a certain grouping strategy might influence how the circuit (in particular its last part) will look like.

Third, there’s a very fundamental issue of deciding how many samples (sometimes also called “shots”) you want to get. For a given problem one sample might be too little, but one million might be way more than necessary. In most cases we just decide on a particular number, e.g. 10000. But to make things even more complicated, you might want to use various numbers of shots for different groups or even change it in different iterations of the optimization loop.

So here’s what our picture looks like now:

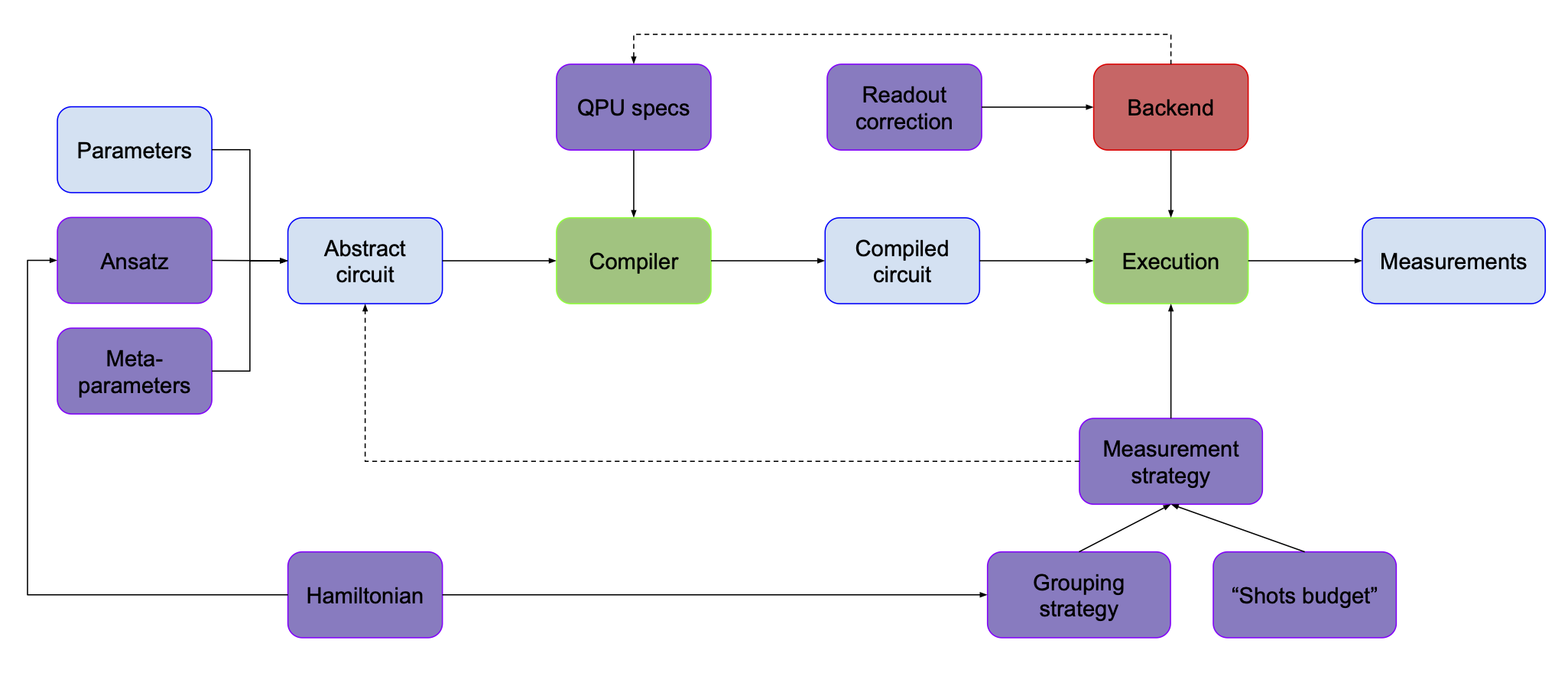
As you can see, I’ve also added a Hamiltonian box. It might influence how our ansatz looks like (e.g. in QAOA) or whether we need to rotate the state before measuring (in VQE), but it also guides the grouping strategy.

So we’re getting the measurements at the end, but are they something that we really care about? Aren’t they just a means to an end? Sure they are! In the case of VQE we want to calculate the expectation value of some operator – for each term you take the measurements, we check what eigenvector they represent and calculate the corresponding eigenvalue (for the details please check out the VQE article). For QAOA we don’t really need to do all that, we can just take the bitstring we got, plug it into the cost function and get the cost value. As you can see, the exact thing that happens here might vary, so let’s just call this part “postprocessing” and agree that it translates all the measurements we got into “energy” or “cost value”.

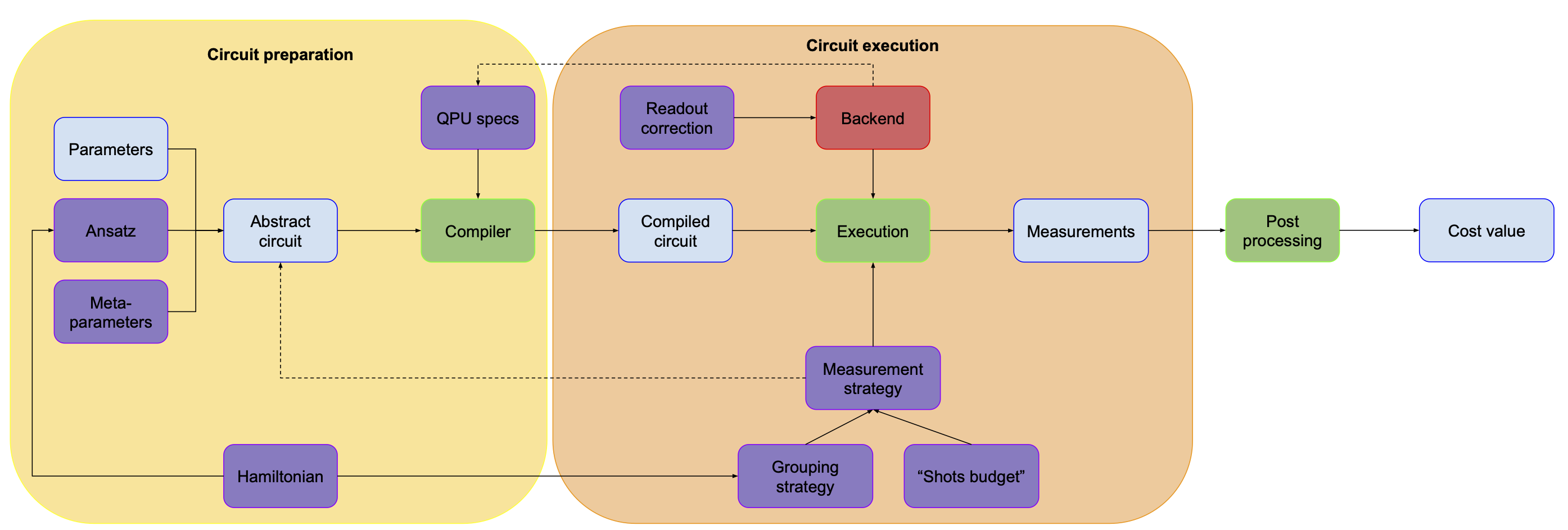
The picture so far can be divided into two parts. One is everything we do to generate a circuit that we’ll run on our hardware. The second one is everything we do with this circuit – how we run it, what we do with the measurements etc. It’s by no means a formal distinction, but I found it helpful to think about it in such a way.

That’s already quite a lot, but we’re just starting! You see, all that we have seen so far is about running a circuit for a single set of parameters. But how do we know which parameters we need to choose?

Glad that you’ve asked!

Welcome to the land of the

Optimization Loop

Basically, the optimization loop looks like this:

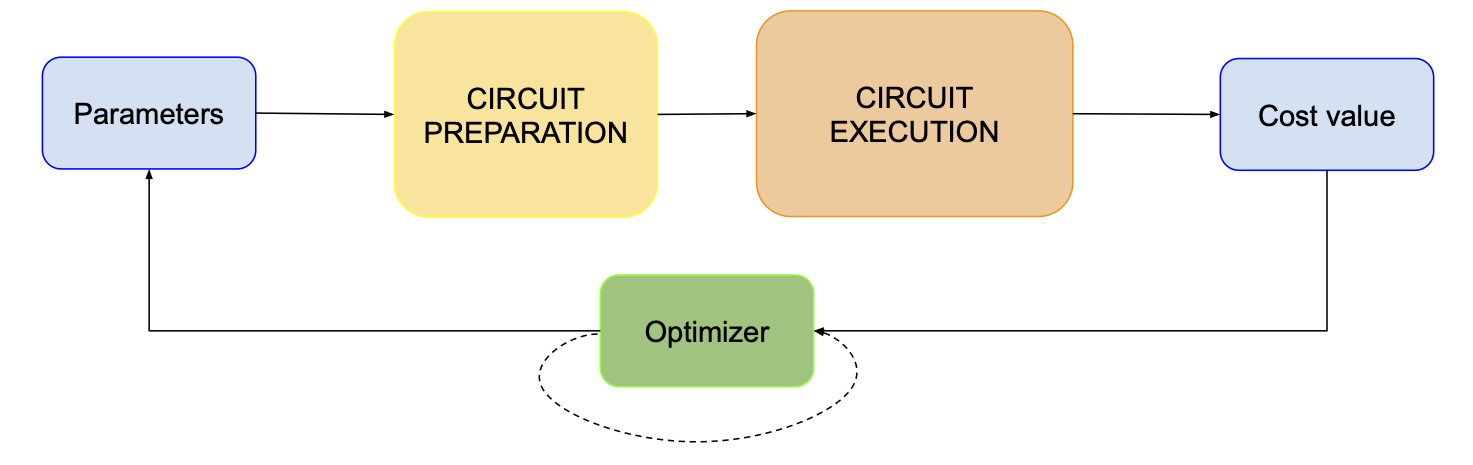
We take some parameters, prepare a circuit based on that, execute and measure that, calculate the energy value and pass it to the optimizer alongside the initial parameters. Given that optimizer can actually need past values to work properly, there’s also this dashed loop around it.

The new block here is “Optimizer”, but actually we haven’t discussed “Parameters” properly yet, so let’s start from that.

Parameters… we know the optimizer updates parameters based on the value of the cost function, but where does the first set of parameters come from? They come from some “parameter initialization” procedure. In order to initialize them, we need to actually know a couple of things:

• How many parameters do we have?
• Are they constrained in any way?
• What method do we want to use for the initialization?

Answers to the first two questions depend specifically on the ansatz that we’re using and the problem we want to solve. For example in the case of QAOA our number of parameters depends solely on the number of layers and not on the problem – we just have a single pair of (\(\beta\), \(\gamma\)) per layer. Also, since our ansatz has periodic behavior with respect to these angles, we might want to constrain them to (\(0\), \(2\pi\)). There’s still the last question to answer – how to choose good initial angles? The most basic method is to just choose them at random, but there are many other methods to get better initial values and it turns out to influence the performance of the algorithm a lot – definitely more than I suspected.

So our picture looks like this now:

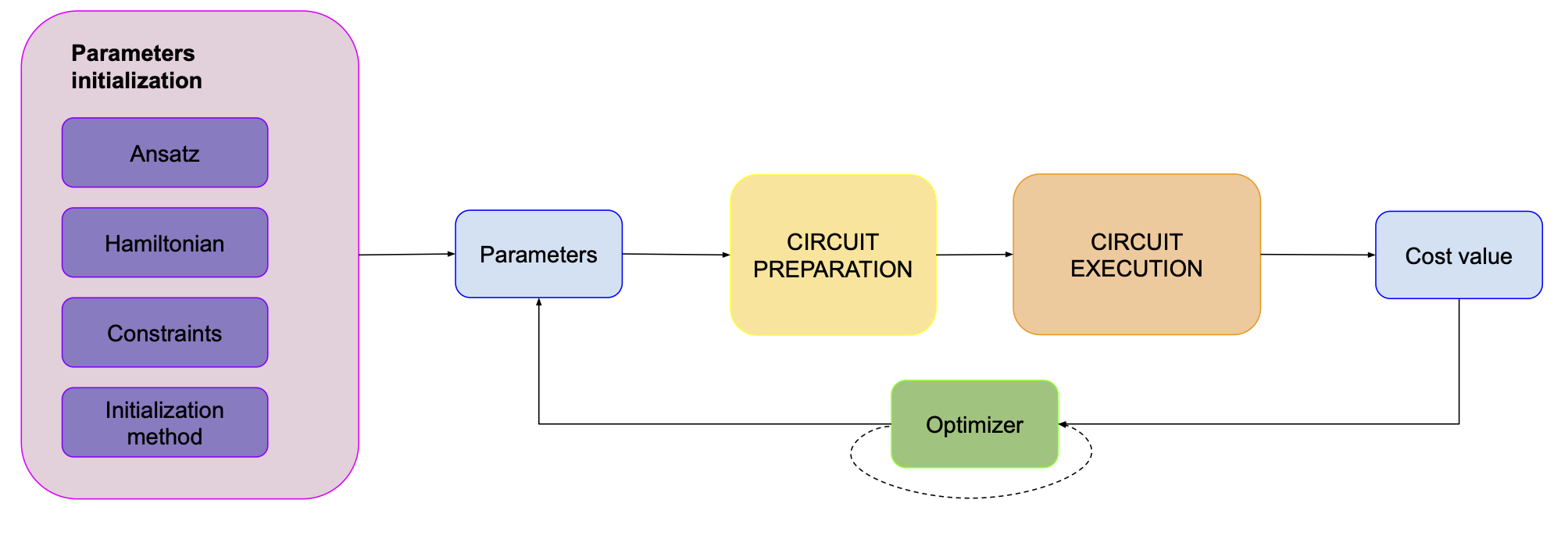
We know initial parameters, we run our circuit, we get some energy value. We pass it to the optimizer and it spits out new parameters. But how does this happen?

Optimizers - gradients

In the process of writing, I have realized that it’s hard to talk about this topic without some basic concepts from the theory of optimization. Let’s say we have some function (we usually call it cost function), which depends on N parameters. Whenever we put these parameters into our function, it returns a single number (in some cases it might be a vector, but that’s uncommon in this context). If we calculated the values of the function for all possible sets of parameters, we would get a full optimization landscape. It’s very convenient to think about it in terms of N-dimensional space, where each set of parameters represents a point (or vector) in such space. Another useful concept is a gradient, which tells us what’s the direction and rate of the fastest increase of the function for any point.

If this sounds abstract, you can think about a map. Our function in this case will take two parameters – latitude and longitude – and return a single value: height. Global (nomen omen) maximum would be Mount Everest and the global minimum Mariana Trench. A steep slope means the gradient is big in that direction, a plateau means it’s small (or even zero). You can generalize such a map to an N-dimensional space and most intuitions still hold.

In the case of the optimization problem, we usually want to find the global minimum and there are many methods to do that. For the sake of simplicity let’s start with a basic one called “gradient descent”. It works as follows:

1. Select a point.
2. Calculate the value of the cost function.
3. Calculate a gradient.
4. Make a step in the direction indicated by the gradient – since we want to get to the minimum, we’re looking for the negative values of the gradient.
5. You’re at a new point, go back to 2.
6. Finish if no further improvement is possible.

Now we’re ready to get back to our VQAs. If we translate this algorithm into the world of VQAs it looks something like this:

1. Select initial parameters
2. Run your circuit and get the energy value.
3. Calculate gradients.
4. Update parameters
5. Go back to 2.
6. Finish if no further improvement is possible.

But how do you calculate gradients? Sometimes we know the exact mathematical formula, but in the case of QC that’s usually not the case. One of the most basic methods to approximate it is called “finite differences”. Let’s say we have a function of one variable \(f(x)\). We can check what’s the value of the gradient by calculating its values at \(f(x+\epsilon)\) and \(f(x-\epsilon)\), where \(\epsilon\) is just a very small number. The gradient is \(g(x) = \frac{1}{2* \epsilon} (f(x+\epsilon) - f(x-\epsilon))\). If we have a function with more variables, we need to check it for various combinations of \(x_i \pm \epsilon\), but the general idea stays the same.

One of the problems with calculating gradients this way is that now we have to evaluate our cost function 3 times every iteration: \(f(x)\), \(f(x+\epsilon)\) and \(f(x-\epsilon)\). If we have more variables, we will need even more evaluations. This might mean that most of your calculations on a quantum computer actually go towards calculating gradients.

Fortunately, there are some other ways of calculating gradients which work better than this. However, some of them might require modifying your circuit. Also, there are some optimizers that don’t even use gradients, but describing all that would be way beyond the scope of this article.

This part was quite lengthy, but it illustrates a couple of points pretty well:

• Notice that there’s nothing “quantum” about the optimization process we used here. In general, most (if not all) of the optimizers used in VQAs don’t really care whether they optimize parameters for quantum computers, neural networks, or a mathematical function. They just care about the input and output.
• There’s actually one thing that is specific for QC (though it doesn’t necessarily apply to quantum only). We have limited precision while calculating the value of the cost function (and its gradients) on a quantum computer, associated with the finite number of measurements.
• It’s easy to miss some big performance issues when you just look at the big picture. For example, if we understood all the pieces of the VQA except for the optimizer we’re using, we could still end up with very bad performance due to a naive method of calculating gradient.
• VQAs have some distinct qualities which make some optimizers work well and some not. For example, every calculation of the cost function is computationally expensive, since you need to use a QPU to get it. Another example is the precision issue that I’ve mentioned above.

Optimizers - other aspects

We have initial parameters, we know how to calculate gradients (or we decide to go with a gradient-free method) so what else do we need to know about the optimizer part?

The first thing is that an optimizer might have multiple hyperparameters, like how big the steps should be in a gradient method or how many iterations do we want to have. These hyperparameters might change throughout the optimization process (if you’re unfamiliar with the concept of hyperparameters, this article might be useful).

Another thing, quite distinct from the optimizer’s parameters, is its constraints. In some cases we might need to put some constraints on the parameters (e.g. they all need to sum up to 1), which influences how the optimizer behaves. An example could be a problem where we know that our quantum state should have a fixed number of particles and our quantum circuit should not represent states with other numbers, even though it’s possible with the ansatz we use.

Lastly, an optimizer might actually modify some of the elements inside the “Circuit preparation/circuit execution” box, most notably the measurement strategy. The easiest example that comes to my mind is the one that I’ve already mentioned, i.e. changing the number of shots during the training. We can argue that in the first iterations when we’re exploring the optimization landscape, we might not need a lot of precision and we can save some QPU time by doing a smaller number of shots. However, once we start converging on the minimum, a small difference in parameters might have huge consequences, so we would rather get higher precision.

So this is what our picture looks like now:

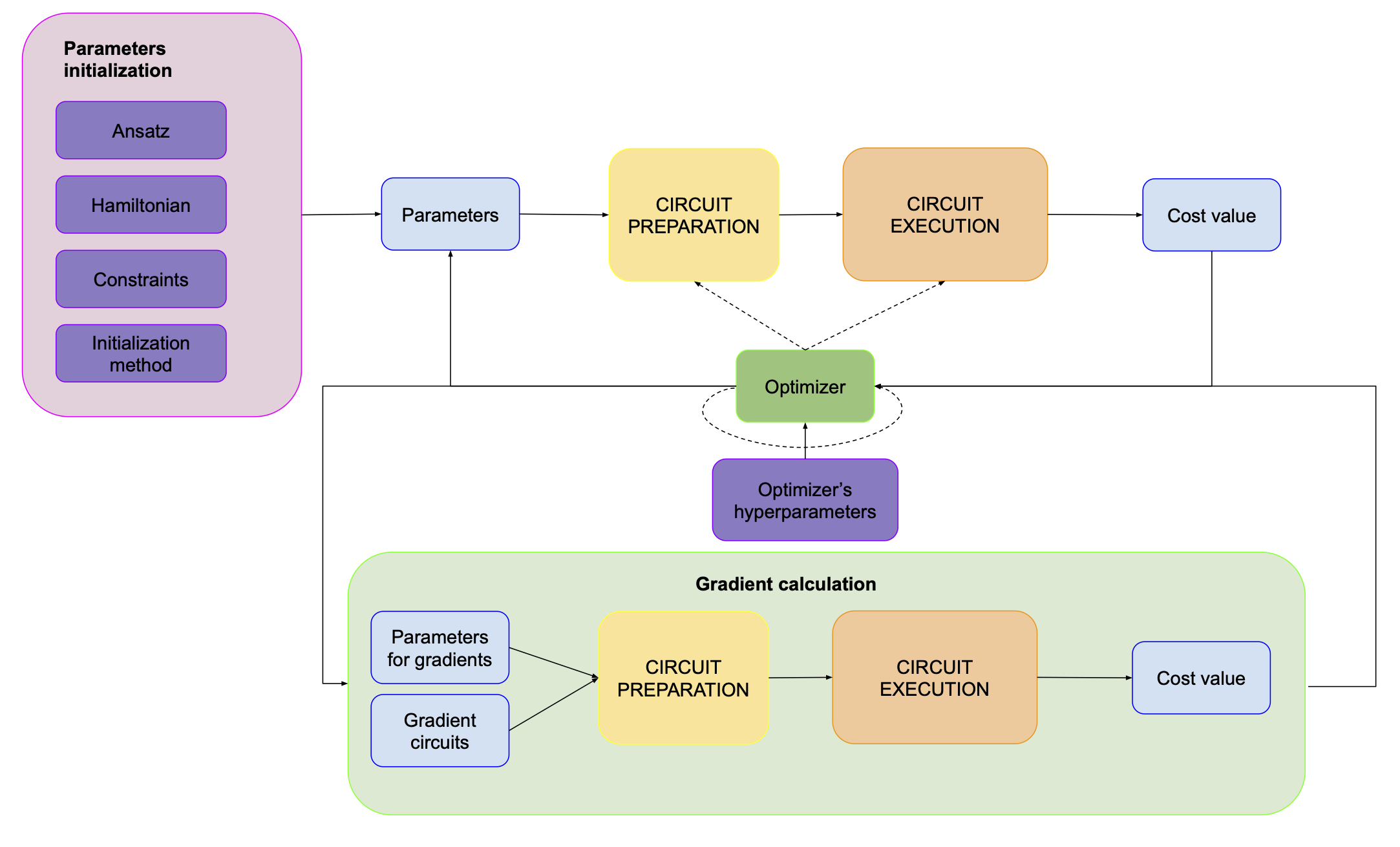
At the bottom, you can see the gradient calculation loop. For the sake of not overcomplicating this plot we’ll hide it inside the optimizer:

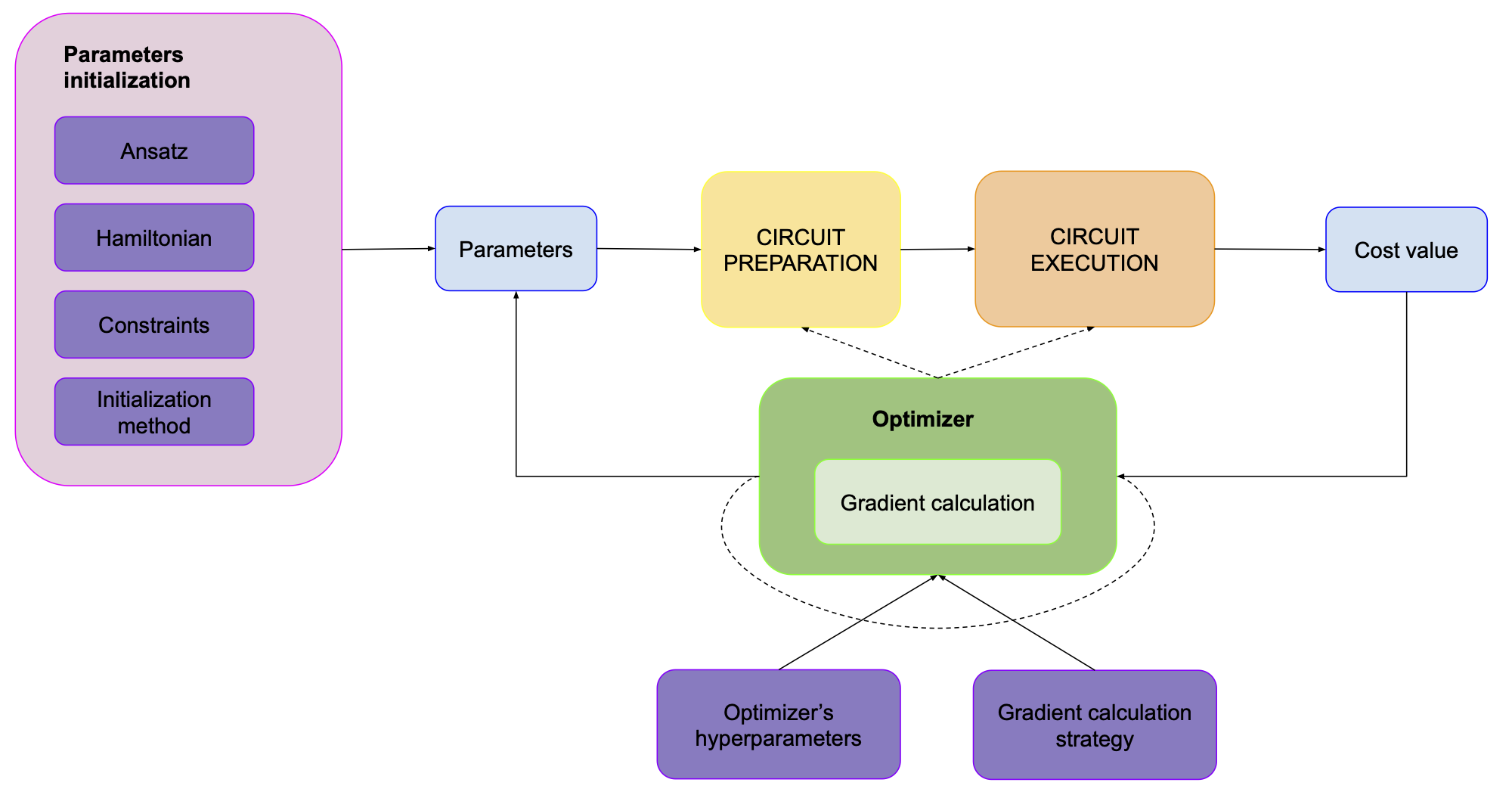
This picture is quite accurate for standard versions of VQAs that you usually encounter. However, I’d like to cover two more cases here, which often show up in the literature

Outside loops

Layer-by-layer training

Many ansatzes (e.g. QAOA) can have multiple layers. One of the problems with many layers is that the more layers you have, the more parameters there are to optimize which means it’s harder to find the optimal values. One of the methods that’s often used to help with that is layer-by-layer training. We first find the optimal parameters for the first layer of our ansatz. We keep them and then add another layer. We optimize the parameters for both layers and then add another.

In such a case our picture would look something like this:

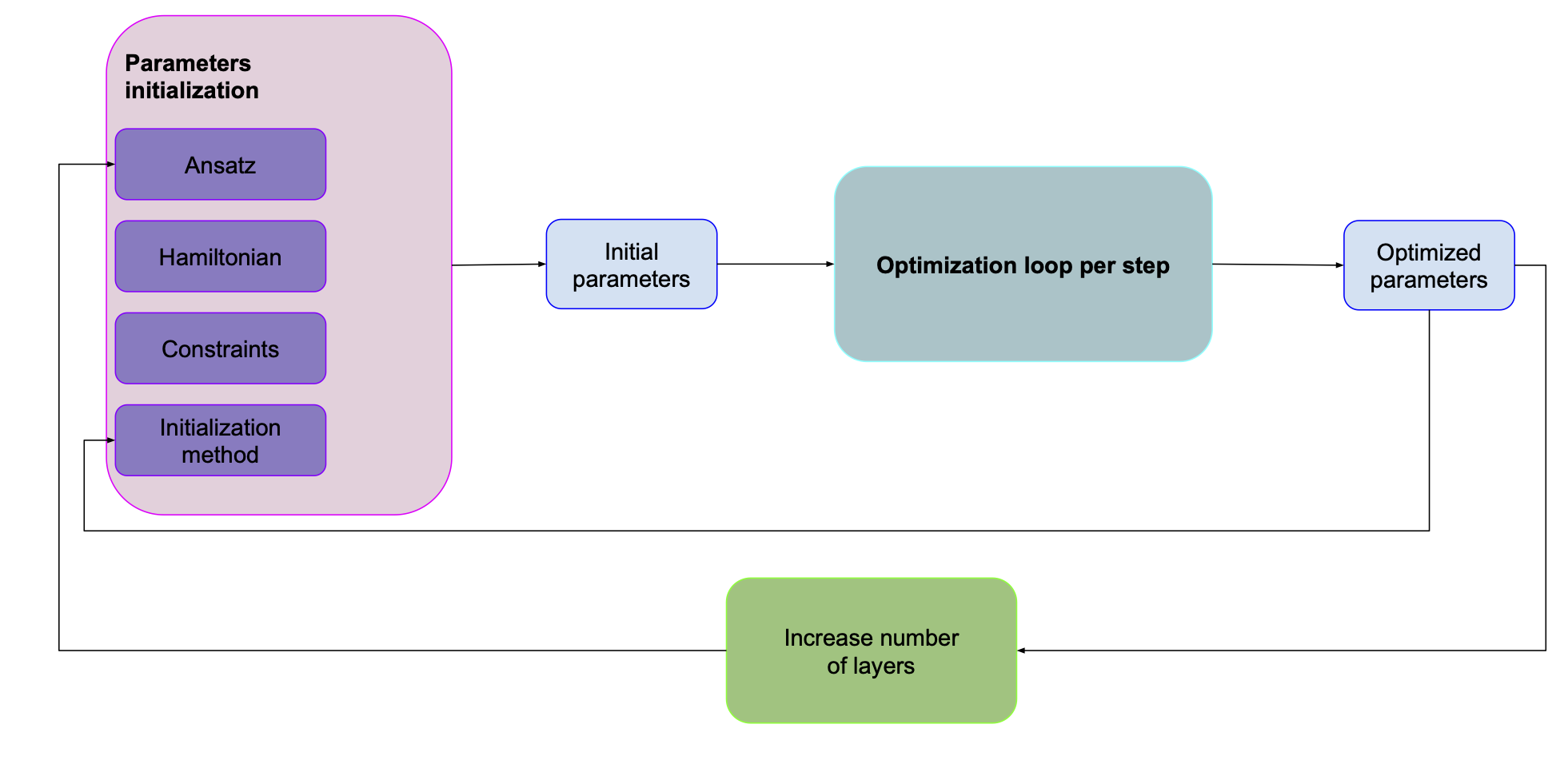
It’s pretty similar to the previous one, except that our parameter initialization strategy depends on the values we found for a smaller number of layers. Obviously, we might also want to change some other parameters like measurement strategy or optimizer hyperparameters.

Adaptive circuits

Recently (2020) there have been many propositions of algorithms which throughout the optimization modify the structure of the circuit itself, not only values of its parameters. As an example I’d like to use the PECT algorithm.

The main idea of this algorithm is that instead of optimizing all the parameters at once, we remove some of the parameters (and the corresponding gates) and optimize only a fraction of the parameters. We have two optimization loops – one selects which parameters we should select for optimization and the other finds the best values of these parameters.

Here we don’t change the structure of the circuit itself, rather just which gates we treat as “parameterizable”. However, there are other proposals as well, where we change the structure of the circuit itself. Actually, layer-by-layer can be treated as an example of such. Another one would be using genetic algorithms to find the optimal ansatz for our problem. Since the structure of the circuit “adapts” during the optimization, such algorithms are sometimes called “adaptive algorithms” (see e.g. Adapt-VQE).

Summary

Look at where you are:

Look at where you started

I tried to make this article comprehensive, but it is actually not getting into too many details. Basically any single element that we discussed can be subject for a separate scientific paper – and many are. If you want to get deeper into specific issue with the VQAs and what are some methods for solving them, I’ve described them in the next article in this series.

If you don’t want to miss any other articles and updates from me, I encourage you to sign up for the newsletter.

I hope you enjoyed reading and it helped you better understand quantum computing in the NISQ era.

As always, I wanted to thank everyone who helped me writing and reviewing:

• Rafał Ociepa
• Jhonathan Romero
• Sukin Sim
• Alba Cervera-Lierta
• Alex Juda
• Stefano Mangini
• Mark Cunningham

Have a nice day!

Michał

---

• All Posts (29) ,
• Quantum computing (20) ,
• Algorithms (6)